Sorting – Bubble sort

Bubble sort:
Two consecutive elements are compared.  It sorts the elements in right to left fashion.  Thus, (n-i) comparisons are made.

Example:

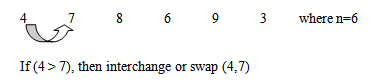
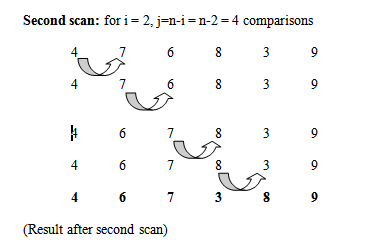
Frequency:

i                       j                       number of times
———————————————————————————————
1                                             1 to n-i                          n-1
2                                             1 to n-i                          n-2
3                                             1 to n-i                          n-3
–                                                  –                                –
–                                                  –                                –
–                                                  –                                –
n-1                                       1 to n-(n-1)                        1

Thus, 1+2+……………+(n-3)+(n-2)+(n-1)

which is sum of (n-1) terms.

=(n-1)(n-1+1)/2
=(n-1)n/2
=n²/2 – n/2
=0.5n²-0.5n

Thus, efficiency in Big(O) Notation is O(n²).

i)  Best Case:  Data is already in sorted form.  Thus no interchange occurs.

Number of comparisons may be reduced as follows:

for i=1,  j=n-i   ie. (n-1)

Frequency is (n-1), which is achieved if we quit after scan, when no interchange occurs.

Hence, efficiency is O(n).

ii)  Worst Case:  Data is in reverse order.  Each value gets interchanged.  Hence number of comparisons will be same as calculated above. i.e.

Efficiency = O(n²)

iii)  Average Case:

(Best Case + Worst Case)/2

= ((n-1) + n²)/2

=(n/2)-(1/2)+(n²/2)

Efficiency = O(n²)

Bubble sort program with n² frequency and an efficiency of O(n²)

#include <stdio.h>
#include <conio.h>

#define n 10

void main()
{
int arr[n], i,j,temp;
clrscr();
printf(“\nInitializing array…!”);
for(i=0;i<n;i++)
{
printf(“\nEnter elements?”);
scanf(“%d”,&arr[i]);
}
for(i=0;i<n-1;i++)
for(j=0;j<n-i-1;j++)
{
if(arr[j]>arr[j+1])
{
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
printf(“\nSorted array using Bubble sort is:\n”);
for(i=0;i<n;i++)
printf(“%d\t”,arr[i]);
getch();
}

Bubble sort program with best efficiency O(n) and frequency (n-1)

#include <stdio.h>
#include <conio.h>

#define n 5

void main()
{
int arr[n], i,j,temp,sort=0;
/*sort=0 for false and sort=1 for true i.e. sorted array*/
clrscr();
printf(“\nInitializing array…!”);
for(i=0;i<n;i++)
{
printf(“\nEnter elements?”);
scanf(“%d”,&arr[i]);
}
for(i=0;i<n-1 && sort!=1;i++)
{
for(j=0;j<n-i-1;j++)
{
sort=1;
if(arr[j]>arr[j+1])
{
sort=0;
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
printf(“\nSorted array using Bubble sort is:\n”);
for(i=0;i<n;i++)
printf(“%d\t”,arr[i]);
getch();
}